随机过程（Stochastic Processes）

这是来自 [2] 的一个随机过程的正式定义：

假设 $(\Omega ,\mathcal{F},P)$ 是一个概率空间，$T\subset \mathbb{R}$ 是一个具有无限基数的集合。进一步假设对于每一个 $t\in T$，都有一个定义在 $(\Omega ,\mathcal{F},P)$ 上的随机变量 $X_t:\Omega \to \mathbb{R}$。

定义函数 $X:T\times \Omega \to \mathbb{R}$，其映射为 $X(t,\omega )=X_t(\omega )$，这个函数被称为一个以 $T$ 为指标集的随机过程，记作： $X=\{X_t,t\in T\}$

这听起来很复杂！我们来分步骤直观解释这个定义。我们在上一小节已经介绍了概率空间和随机变量。

随机过程的第一层含义是：我们有一组用某个集合 $T$ 编号的随机变量。通常 $T$ 是一个全序集合，例如实数的子集（如 $(0,\infty )$）或自然数（如 $0,1,2,3,\dots$），对应于连续时间或离散时间。

接下来我们关注每个随机变量所依赖的概率空间 $(\Omega ,\mathcal{F},P)$。关键在于样本空间中的元素 $\omega \in \Omega$ 是一个无限序列，对应于在 $T$ 的每个时刻执行一次实验。（注意：由于是无限个实验，否则这只是一个随机向量。）

例如，从 $t=0$ 到 $t=\infty$ 每次掷硬币，将产生一个具体的无限序列 $\omega =\{H,T,H,H,H,T,\dots \}$。 每个随机变量 $X_t$ 都是从这个无限实验序列中提取某些信息并映射到实数子集的函数 $X_t:\Omega \to E\subseteq \mathbb{R}$。 需要注意的是，这种通用定义中并没有显式包含“时间方向”的概念，因此可以包含对“未来”的依赖。为了包含通常意义下的时间因果性，我们还需引入“适应性过程（adapted process）”等额外概念（后文会介绍）。

从另一视角，我们可以将随机过程看作关于时间 $t$ 和样本 $\omega$ 的联合函数 $X(t,\omega )=X_t(\omega )$。 对于某一次具体实验结果 ${\omega }_0$，我们就得到了一个样本路径函数 $X(t,\omega ={\omega }_0)$，这是一个确定性的函数。但在多数情形下，我们习惯使用集合形式的记法来表示一个时序上的随机变量序列 $X=\{X_t,t\in T\}$。 有时也用简记形式 $X(t)$ 来表示时刻 $t$ 上的随机变量或整个随机过程。

随机过程可以依据值域类型与指标集类型分类如下：

• 离散值/连续值过程（Discrete/Continuous Value Process）：当每个 $X(t)$ 的取值属于一个可数集合（例如自然数的子集）时，称该过程为离散值过程；否则为连续值过程。

• 离散时间/连续时间过程（Discrete/Continuous Time Process）：当指标集 $T$ 为一个可数集合时，称该过程为离散时间过程；否则为连续时间过程。

通常情况下，连续时间过程的分析更为复杂，而本文后续章节将主要聚焦于此。下面两个离散时间过程示例将帮助我们更好地从形式定义过渡到具体情形的直觉理解。

例 2: Bernoulli 过程

最简单的随机过程之一是 Bernoulli 过程，它是一个离散取值、离散时间的过程。其核心思想是在每一个时间点进行一次独立同分布的伯努利试验（可类比为抛硬币）。

更正式地说，我们的样本空间为： $\Omega =\left\{(a_n{)}_{n=1}^{\infty }:a_n\in \{H,T\}\right\}$ 表示由“正面（H）”与“反面（T）”构成的无限序列集合。
事件空间与概率测度的精确定义较为复杂，这部分内容将在附录 A 中详细讨论。

现在，给定一次无限投掷的结果 $\omega$，我们可以定义如下的随机变量：

$$X_t(\omega )=\{\begin{array}{ll}1& \text{if }{\omega }_t=H\\ & \\ -1& \text{otherwise}\end{array}\text{\hspace{1em}(2.7)}$$

其中，$\omega ={\omega }_1,{\omega }_2,{\omega }_3,\dots$ 是一次实验结果序列，而每个 ${\omega }_i$ 表示第 $i$ 次投掷的结果。

对于任意 $t$，我们有 $P(X_t=1)=p$， 且 $p\in [0,1]$， 表示抛出“正面”的概率为常数 $p$，该概率在整个过程中保持不变。

例 3: 一维对称随机游走

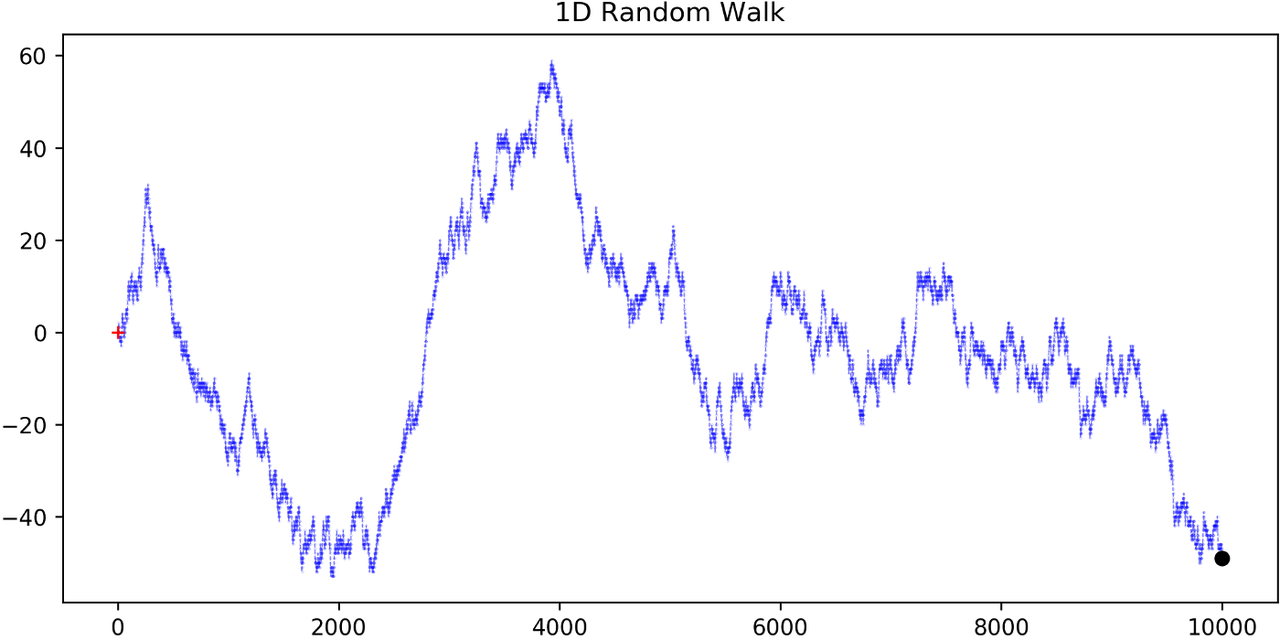
一个最简单的一维对称随机游走，是一种离散值、离散时间的随机过程。你可以把它想象成：从 0 开始，每一步抛一次公平的硬币，若正面则向上移动（+1），否则向下移动（-1）。

图 1: 一维对称随机游走 (图片来源)

该过程可以用上一节的伯努利过程 $X_t$（令 $p=0.5$）来定义：

$$S_t(\omega )=\sum _{i=1}^t{X}_i(\omega )\text{\hspace{1em}(2.8)}$$

你会注意到，$S_t$ 在每个时间点的取值，依赖于所有先前的“抛硬币结果” $X_i$，这与伯努利过程中每一步只依赖当前时刻不同。

接下来是两个我们将在后面使用的重要结论。

首先，对于任意不重叠的整数区间对 $0=k_0<k_1<k_2<\cdots <k_m$ 所构成的增量变量，如 $(S_{k_1}-S_{k_0}),(S_{k_2}-S_{k_1}),\dots ,(S_{k_m}-S_{k_{m-1}})$ 是相互独立的。这是因为各个差分段只涉及不重叠的 $X_t$，而这些 $X_t$ 本身是独立的。

此外，增量的期望值与方差如下：

$$\begin{array}{rl}\mathbb{E}[S_{k_{i+1}}-S_{k_i}]& =\mathbb{E}\left[\sum _{j=k_i+1}^{k_{i+1}}{X}_j\right]\\ & \\ & =\sum _{j=k_i+1}^{k_{i+1}}\mathbb{E}[X_j]\\ & \\ & =0\\ & \\ \mathrm{Var}[S_{k_{i+1}}-S_{k_i}]& =\mathrm{Var}\left[\sum _{j=k_i+1}^{k_{i+1}}{X}_j\right]\\ & \\ & =\sum _{j=k_i+1}^{k_{i+1}}\mathrm{Var}[X_j]\text{（}{X}_j\text{ 独立）}\\ & \\ & =\sum _{j=k_i+1}^{k_{i+1}}1\text{（}\mathrm{Var}[X_j]=\mathbb{E}[X_j^2]=1\text{）}\\ & \\ & =k_{i+1}-k_i\end{array}\text{\hspace{1em}(2.9)}$$

这意味着，对称随机游走的方差以“每步一步”的速率线性增长。如果从当前位置再走 $l$ 步，那么对应的方差为 $l$。这一规律在后续我们探讨连续时间扩展时会再次出现。