Wiener 过程（Wiener Process）

Wiener 过程（也称为布朗运动）是最被广泛研究的连续时间随机过程之一，它频繁出现在诸如应用数学、量化金融和物理学等多个领域中。正如我们之前所提到的，它具有许多“边界情况”的性质，这些性质使得该过程无法通过简单的方法进行处理，也正是因为这些问题，才催生了随机微积分的发展。值得注意的是，Wiener 过程存在多个等价的定义，而我们将从参考文献 [1] 中给出的一个定义出发，该定义使用了缩放的对称随机游走（scaled symmetric random walk）过程。

缩放对称随机游走（Scaled Symmetric Random Walk）

缩放的对称随机游走是我们在例 3 中所展示的简单随机游走的一种扩展，我们将“加快时间”并“缩小步长”，从而将其扩展到连续时间。更准确地说，对于一个固定的正整数 $n$，我们定义如下的缩放随机游走过程：

$$W^{(n)}(t)=\frac{1}{\sqrt{n}}{S}_{nt}\text{\hspace{1em}(2.13)}$$

其中 $S_{nt}$ 是一个简单的对称随机游走过程，前提是 $nt$ 是一个整数。如果 $nt$ 不是整数，我们则通过线性插值来定义 $W^{(n)}(t)$。

一个直观的理解方式是：公式 2.13 本质上就是一个带缩放因子的普通随机游走。例如，$W^{(100)}(t)$ 的第一次整数步长发生在 $t=\frac{1}{100}$ 而不是 $t=1$。为了调整这种时间压缩的影响，我们对过程施加 $\frac{1}{\sqrt{n}}$ 的缩放因子（稍后会更详细地讨论其原因）。线性插值的部分本身并不重要，只是我们希望在连续时间中进行操作。下图展示了这一缩放随机游走的可视化结果：

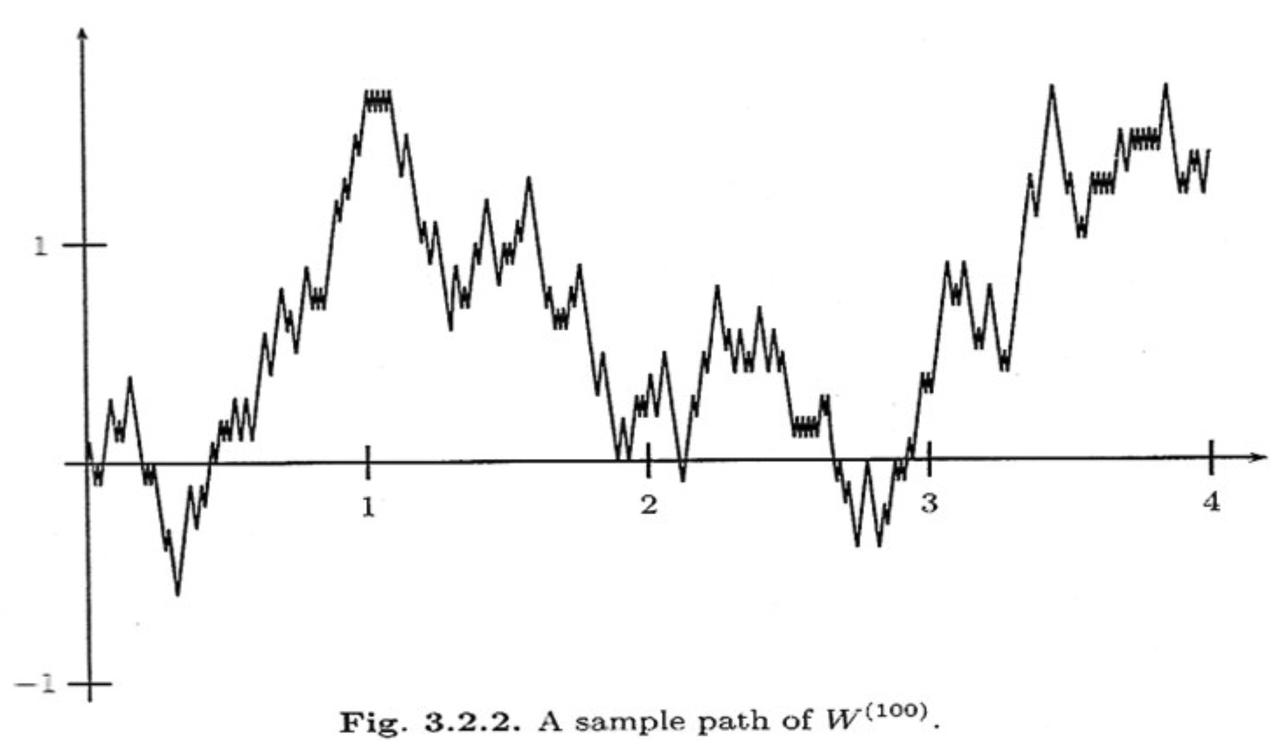
图 2：缩放的对称随机游走（图片来源）

由于这仍然只是一个简单的对称随机游走（假设我们观察的是整数步），因此与例 3 中讨论的性质一致：非重叠增量彼此独立。此外，对于 $0\le s\le t$，我们有：

$$\begin{array}{rl}\mathbb{E}\left[W^{(n)}(t)-W^{(n)}(s)\right]& =0\\ \mathrm{Var}\left[W^{(n)}(t)-W^{(n)}(s)\right]& =t-s\end{array}\text{\hspace{1em}(2.14)}$$

这里我们使用了平方根缩放，使得方差仍然以单位时间为增量进行积累。

另一个重要性质被称为二次变差，它是沿某一特定路径计算的（即没有随机性）。对于某一已知路径的缩放对称随机游走过程，我们有：

$$\begin{array}{rl}[W^{(n)},W^{(n)}{]}_t=& \sum _{j=1}^{nt}{\left(W^{(n)}\left(\frac{j}{n}\right)-W^{(n)}\left(\frac{j-1}{n}\right)\right)}^2\\ =& \sum _{j=1}^{nt}{\left(\frac{1}{\sqrt{n}}{X}_j\right)}^2\\ =& \sum _{j=1}^{nt}\frac{1}{n}=t\end{array}\text{\hspace{1em}(2.15)}$$

我们得到的结果与公式 2.14 中的方差一致（当 $s=0$ 时），但在概念上它们是不同的。方差是对所有路径的平均，而二次变差是在某条已实现路径上，取所有增量的平方并求和。在 Wiener 过程的特殊情形下，它们结果一致（但对于一般的随机过程并不一定成立）。

最后，正如你所料，我们希望理解当 $n\to \infty$ 时，这种缩放的随机游走过程将如何变化。对于固定的 $t\ge 0$，我们回顾以下事实：

• $\mathbb{E}\left[W^{(n)}(t)\right]=0$（由公式 2.14 设 $s=0$ 得出）；
• $\mathrm{Var}\left[W^{(n)}(t)\right]=t$（同上）；
• $W^{(n)}(t)=\frac{1}{\sqrt{n}}{\sum }_{i=1}^t{X}_t$，其中 $X(t)$ 是伯努利过程；
• 根据中心极限定理：

$$\frac{1}{\sqrt{n}}\sum _{i=1}^n{Y}_i\stackrel{d}{\to }\mathcal{N}({\mu }_Y,{\sigma }_Y^2)$$

其中 $Y_i$ 是独立同分布的随机变量，且满足一定条件。

我们可以看出，缩放的对称随机游走过程完全满足中心极限定理的条件，因此当 $n\to \infty$ 时，$W^{(n)}(t)$ 收敛于均值为 $0$、方差为 $t$ 的正态分布。这正是我们在下一节中用来定义 Wiener 过程的方法。

Wiener 过程定义

我们终于来到了 Wiener 过程的定义，这个过程是前面所述的“缩放对称随机游走”在 $n\to \infty$ 时的极限形式。我们将依据这个极限定义的分布性质来定义 Wiener 过程，这些性质大多是从“缩放对称随机游走”中继承而来：

给定概率空间 $(\Omega ,\mathcal{F},P)$，假设存在一个关于 $t\ge 0$ 的连续函数，并且也依赖于 $\omega \in \Omega$，我们将其记作： $W(t):=W(t,\omega )$

若满足以下条件，则 $W(t)$ 是一个 Wiener 过程：

1. 初始值为零： $W(0)=0$
2. 所有不重叠的增量都是独立的，即对于任意满足 $0=t_0<t_1<\cdots <t_{m-1}<t_m$，有以下增量： $W(t_1)-W(t_0),\dots ,W(t_m)-W(t_{m-1})$ 互相独立；
3. 每个增量都是正态分布，且具有期望 $E\left[W(t_{i+1})-W(t_i)\right]=0$ 与方差 $\mathrm{Var}\left[W(t_{i+1})-W(t_i)\right]=t_{i+1}-t_i$。

我们可以看到，Wiener 过程继承了缩放对称随机游走的许多性质，尤其是增量独立与增量服从正态分布。不过，Wiener过程的增量是严格的正态分布，而不是像前面的随机游走那样只是在大 $n$ 情况下近似正态。

我们可以从物理的角度理解 Wiener 过程：每个 $\omega$ 表示一个随机路径，比如悬浮在液体中的粒子的随机运动。每一个时间的无限小片段，粒子都会被随机扰动（且扰动服从正态分布）而改变方向。这正是植物学家 Robert Brown 最早观察到的布朗运动现象的数学模型，后来爱因斯坦等人对其进行了严格的数学建模。

另一种理解方式是“硬币抛掷”：我们可以认为 $\omega$ 是一系列无限快发生的硬币抛掷结果——不像之前的模型只在整数时间点发生，而是在每一个无限小的时间片段中发生。这正是取极限的结果。

此时，我们可以对 Wiener 过程在任意时间点 $t$ 提出我们对随机变量的所有典型问题。下面我们就来看一个简单的例子。

例5：Wiener 过程概率计算

假设我们希望求出 Wiener 过程在 $t=0.25$ 时，其值落在区间 $[0,0.2]$ 内的概率。

换句话说，我们希望计算如下事件的概率： $A\in \mathcal{F}$，使得 $\omega \in A\Rightarrow 0\le W(0.25)\le 0.2$

我们知道Wiener过程在区间 $[0,0.25]$ 上的增量服从： $$W(0.25)-W(0)=W(0.25)\sim \mathcal{N}(0,0.25)\text{\hspace{1em}(2.16)}$$ 因此我们只是想求一个正态分布落在特定区间内的概率。根据正态分布密度函数公式： $$\begin{array}{rl}P(0\le W(0.25)\le 0.2)=& \frac{1}{\sqrt{2\pi \cdot 0.25}}{\int }_0^{0.2}\exp \left(-\frac{1}{2}{\left(\frac{x}{\sqrt{0.25}}\right)}^2\right)dx\\ =& \frac{2}{\sqrt{2\pi }}{\int }_0^{0.2}\exp (-2x^2)dx\\ \approx & 0.155\end{array}\text{\hspace{1em}(2.17)}$$

我们还需要讨论Wiener过程的滤波（filtration）。定义与前面章节相同，但我们要额外强调：未来的增量必须独立于当前的 ${\mathcal{F}}_t$ 信息。

正是因为后面我们会将更复杂的自适应过程作为被积函数（integrand），并以Wiener过程作为积分器进行积分，所以这种“未来不可预知性”是合理性的核心。这是为了防止被积过程“看到未来”。

Wiener过程的二次变差（Quadratic Variation）

我们之前在讨论缩放后的对称随机游走（scaled symmetric random walk）时提到，其二次变差随时间线性累积，即在区间 $[0,T]$ 上的总二次变差为 $T$，且这一结论与分割数 $n$ 无关。我们将看到，这一现象对于 Wiener 过程也成立。但在此之前，我们先来思考为什么这件事看起来很奇怪。

设函数 $f(t)$ 定义在区间 $[0,T]$ 上。它在 $[0,T]$ 上的二次变差（quadratic variation）定义为：

$$[f,f](T)=\underset{\Vert \Pi \Vert \to 0}{\lim }\sum _{j=0}^{n-1}{\left[f(t_{j+1})-f(t_j)\right]}^2\text{\hspace{1em}(2.18)}$$

其中，$\Pi =\{t_0,t_1,\dots ,t_n\}$ 是对区间 $[0,T]$ 的划分，满足： $0\le t_1\le t_2<\cdots <t_n=T$， 且 $\Vert \Pi \Vert$ 表示分割的网格大小（mesh），即 $\Vert \Pi \Vert ={\max }_{j=0,\dots ,n}(t_{j+1}-t_j)$

这个定义的核心思想和我们之前讨论的类似：对每个小区间取函数值之差的平方，再将所有区间相加。与黎曼积分（Riemannian integrals）定义类似（尽管我们通常不是这样学习的），只不过这里的划分可以是不均匀的，只要网格趋于0即可。

现在我们有了式 (2.18)，让我们看看它作用在一个可导函数上时会发生什么。根据均值定理（Mean Value Theorem）： 若 $f(x)$ 在区间 $(a,b)$ 上可导且连续，则存在 $c\in (a,b)$，使得： $f^{\prime }(c)=\frac{f(a)-f(b)}{b-a}$。 在此基础上，对有连续导数的函数 $f(t)$，其二次变差推导如下：

$$\begin{array}{rl}[f,f](T)& =\underset{\Vert \Pi \Vert \to 0}{\lim }\sum _{j=0}^{n-1}[f(t_{j+1})-f(t_j){]}^2\text{（定义）}\\ & =\underset{\Vert \Pi \Vert \to 0}{\lim }\sum _{j=0}^{n-1}|f^{\prime }(t_j^{\ast }){|}^2(t_{j+1}-t_j{)}^2\text{（均值定理）}\\ & \le \underset{\Vert \Pi \Vert \to 0}{\lim }\Vert \Pi \Vert \cdot \sum _{j=0}^{n-1}|f^{\prime }(t_j^{\ast }){|}^2(t_{j+1}-t_j)\\ & =(\underset{\Vert \Pi \Vert \to 0}{\lim }\Vert \Pi \Vert )\cdot (\underset{\Vert \Pi \Vert \to 0}{\lim }\sum _{j=0}^{n-1}|f^{\prime }(t_j^{\ast }){|}^2(t_{j+1}-t_j))\text{（极限乘法法则）}\\ & =(\underset{\Vert \Pi \Vert \to 0}{\lim }\Vert \Pi \Vert )\cdot {\int }_0^T|f^{\prime }(t){|}^{2}dt=0\text{（当 }\Vert \Pi \Vert \to 0\text{ 且 }{f}^{\prime }(t)\text{ 连续时）}\end{array}\text{\hspace{1em}(2.19)}$$

这表明，对于我们日常中遇到的那些具有连续导数的函数，其二次变差为0，即几乎没有实际意义。 但对于 Wiener 过程来说，其路径处处连续却处处不可导，因此我们无法像 (2.19) 那样使用均值定理。

为此我们来看一个更简单的例子：图3 所示的绝对值函数 $f(t)=|t|$。

在区间 $(-2,5)$ 上，我们可以计算两个端点之间的平均斜率为 $\frac{3}{7}$。 但在整个区间内，函数 $f(t)=|t|$ 的导数永远不会等于$\frac{3}{7}$：要么是 $1$，要么是 $-1$，在 $t=0$ 处导数甚至不存在。因此，该函数并没有一处导数值恰好等于 $\frac{3}{7}$。

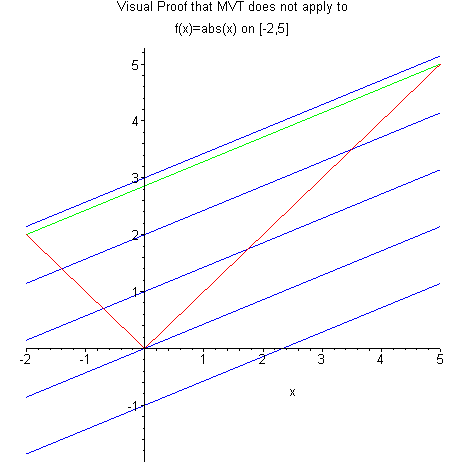
图3：均值定理无法用于不可导函数 (图片来源)

这与我们在缩放对称随机游走中遇到的情况很相似——每两个离散点之间我们都采用线性插值，但无论怎么插值，随着分割数 $n$ 增加，这种“尖角”行为仍然存在，并最终在极限中被 Wiener 过程继承。

因此我们要面对这样一种函数：处处连续却处处不可导。这正是我们需要随机微积分（Stochastic Calculus）的根本原因之一——否则我们本可以使用熟悉的经典微积分法则。

定理 1

对于Wiener过程 $W$，其二次变差为 $[W,W](T)=T$，对所有 $T\ge 0$ 几乎必然成立。

证明

定义如下采样的二次变差（参考公式 2.18）：

$$Q_{\Pi }=\sum _{j=0}^{n-1}{\left(W(t_{j+1})-W(t_j)\right)}^2\text{\hspace{1em}(2.20)}$$

这个量是一个随机变量，因为它依赖于Wiener过程的特定“结果路径”（回顾下二次变差是相对于某一条实际路径定义的）。

为了证明该定理，我们需要证明，当分割的粒度趋于 0 时，采样的二次变差 $Q_{\Pi }\to T$。 我们只需证明 $\mathbb{E}[Q_{\Pi }]=T\text{且}\text{Var}[Q_{\Pi }]=0$。 这意味着，无论路径如何，$Q_{\Pi }$ 都收敛于 $T$。

我们知道Wiener过程的每个增量彼此独立，因此其总和的期望值和方差就是各个增量期望值和方差的总和。

已知（根据Wiener过程定义）：

$$\begin{array}{rl}\mathbb{E}[(W(t_{j+1})-W(t_j){)}^2]& =\mathbb{E}[(W(t_{j+1})-W(t_j){)}^2]-0\\ & =\mathbb{E}[(W(t_{j+1})-W(t_j){)}^2]-\mathbb{E}[W(t_{j+1})-W(t_j){]}^2\\ & =\mathrm{Var}[W(t_{j+1})-W(t_j)]\\ & =t_{j+1}-t_j\end{array}\text{\hspace{1em}(2.21)}$$

所以我们可以计算：

$$\begin{array}{rlr}\mathbb{E}[Q_{\Pi }]& =\mathbb{E}[\sum _{j=0}^{n-1}(W(t_{j+1})-W(t_j){)}^2]& \\ & =\sum _{j=0}^{n-1}\mathbb{E}[(W(t_{j+1})-W(t_j){)}^2]& \\ & =\sum _{j=0}^{n-1}(t_{j+1}-t_j)& \text{公式 2.21}\\ & =T& \end{array}\text{\hspace{1em}(2.22)}$$

再由已知结论（正态随机变量四阶矩期望为 3 倍方差）可得：

$$\mathbb{E}[(W(t_{j+1})-W(t_j){)}^4]=3\cdot \text{Var}[(W(t_{j+1})-W(t_j){)}^2]=3(t_{j+1}-t_j{)}^2\text{\hspace{1em}(2.23)}$$

接着我们来计算单个增量的平方差的方差：

$$\begin{array}{rl}\mathrm{Var}[(W(t_{j+1})-W(t_j){)}^2]& =\mathbb{E}{\left[((W(t_{j+1})-W(t_j){)}^2-\mathbb{E}[(W(t_{j+1})-W(t_j){)}^2]\right)}^2\\ & =\mathbb{E}\left[((W(t_{j+1})-W(t_j){)}^2-(t_{j+1}-t_j){)}^2\right]\\ & =\mathbb{E}[(W(t_{j+1})-W(t_j){)}^4]\\ & -2(t_{j+1}-t_j)\mathbb{E}[(W(t_{j+1})-W(t_j){)}^2]\\ & +(t_{j+1}-t_j{)}^2\\ & =3(t_{j+1}-t_j{)}^2-2(t_{j+1}-t_j{)}^2+(t_{j+1}-t_j{)}^2\\ & =2(t_{j+1}-t_j{)}^2\end{array}\text{\hspace{1em}(2.24)}$$

最终我们可以计算 $Q_{\Pi }$ 的方差：

$$\begin{array}{rlr}\mathrm{Var}[Q_{\Pi }]& =\sum _{j=0}^{n-1}\mathrm{Var}\left[(W(t_{j+1})-W(t_j){)}^2\right]& \\ & =\sum _{j=0}^{n-1}2(t_{j+1}-t_j{)}^2& \text{公式 2.24}\\ & \le \sum _{j=0}^{n-1}2\Vert \Pi \Vert (t_{j+1}-t_j)& \\ & =2\Vert \Pi \Vert T& \text{公式 2.22}\end{array}\text{\hspace{1em}(2.25)}$$

由于我们设定 $\Vert \Pi \Vert \to 0$，即每段长度趋于 0，而个数趋于无穷，那么这个和将趋于 0，所以 $\text{Var}[Q_{\Pi }]\to 0$。 因此，$Q_{\Pi }\to T$ 几乎必然成立，定理得证。

术语 几乎必然（almost surely）是一个技术术语，意思是“概率为1”。这在处理无穷时是另一个直觉上难以理解的概念。定理并不是说没有具有不同二次变差的路径，而是说这些路径在无穷多个路径中是可以忽略的，因此它们的概率为零。

从更高层次看，这是一个非常深刻的结果：如果你取 Wiener 过程中的任意一条实际路径，对其无限小的平方增量求和，其和几乎必然等于区间的长度。换句话说，Wiener 过程以每单位时间积累一个单位的二次变差。

这可能让人惊讶，因为它可以是任意一条路径。无论“无限快”的硬币掷出的结果如何，平方增量之和总会趋近于区间长度。尽管路径是连续的（但没有连续导数），最终结果非零，这也令人惊讶，如我们上面所讨论的。

我们通常会非正式地写成：

$$dW(t)dW(t)=dt\text{\hspace{1em}(2.26)}$$

来描述以单位速率积累二次变差。然而，这不应被理解为对每一个无限小增量都成立。请记住，$W(t)$ 的每个增量是正态分布的，所以等式左边实际上是一个正态分布变量的平方。我们只有在对大量增量求和时，才会得到定理1的结果（详情见[1]）。

我们还可以用这种非正式记号来描述一些相关概念：交叉变差（公式 2.27）和时间变量的二次变差（公式 2.28）分别为：

$$dW(t)\cdot dt=0\text{\hspace{1em}(2.27)}$$

$$dt\cdot dt=0\text{\hspace{1em}(2.28)}$$

时间的二次变差可以用上文公式 2.18 中的定义，而交叉变差则是使用两个不同的函数（$W(t)$ 和 $t$），而不是同一个函数。直观地，这两个变差都是0，因为时间增量 $\Pi$ 在极限中趋近于0，因此这两个变差也随之趋近于0。这可以用与前述二次变差类似的论证更正式地证明（详见[1]）。

Wiener 过程的首次到达时间（First Passage Time）

我们在这里插入一个非直观的性质来说明 Wiener 过程：它最终必然会达到某个给定的水平 $m$。

定理 2

对于 $m\in \mathbb{R}$，Wiener 过程达到水平 $m$ 的首次到达时间 ${\tau }_m$ 几乎必然是有限的，也就是说， $P({\tau }_m<\infty )=1$

这基本上说明，Wiener 过程几乎肯定会在某个有限时间 ${\tau }_m$ 内达到任意一个有限水平 $m$。换句话说，虽然确实存在一些路径使得 Wiener 过程永远不达到这个水平 $m$，但这些路径的集合是如此微小，以至于它们的概率为 0（即几乎必然不会发生）。处理无穷时确实常常带来一些不直观的结果。